Los Números Enteros (Z)

Historia.

Los números enteros positivos y negativos, son el resultado Natural de las operaciones suma y resta.

El Nombre ENTERO se justifica porque los números positivos o negativos, siempre representaban una cantidad de Unidades no divisibles.

Los griegos utilizaron reglas similares a las usadas en la actualidad para realizar operaciones aritméticas con magnitudes negativas en sus demostraciones geométricas, sin embargo el merito de transformar esas pautas en reglas numéricas positivos, negativos y cero (0) corresponde a los Hindúes en los años 650 a.C.

Números Enteros.

Los números enteros son un conjunto de números que abarcan a los números naturales incluyendo al cero(0) y los números negativos (-1, -2, etc)

Los números enteros son aquellos que no tienen parte decimal. 

Por ejemplo: 4,55 (NO ES UN NUMERO ENTERO)

Los números enteros negativos tienen diversas aplicaciones practicas. Con ello se puede señalar una temperatura baja de cero.

Por Ejemplo:  " En estos momentos la temperatura en el Pico Bolívar de Mérida es -5°C.

Al igual que los números naturales, los números enteros pueden: Sumarse, Restarse, Multiplicarse y Dividirse.

Sin embargo en el caso de los Números Enteros es necesario calcular también el signo del resultado.

Los números Enteros extienden la utilidad de los números Naturales para contar cosas, también puede utilizarse para contabilizar perdidas.

Suma de Números Enteros:

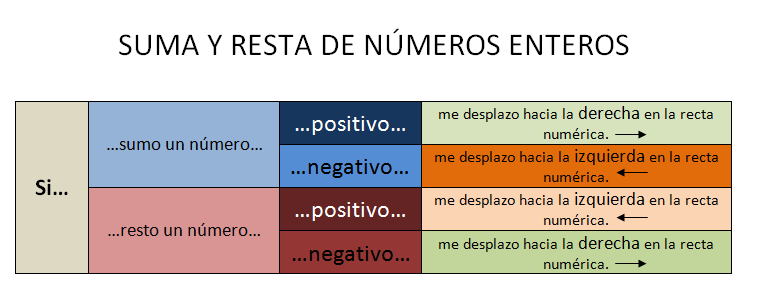
Para Sumar números enteros se procede del siguiente modo:

Ä    Si tienen el mismo signo, se suman sus valores absolutos, u al resultado se le pone el signo que tenían los sumando:

7 + 11 = 18

-7 – 11 = -18

Ä    Si tienen distintos signos, es decir, si un sumando es positivo y el otro es Negativo, se restan sus valores absolutos y se e coloca el signo de mayor:

7 + (5) = 7 – 5 = -2

-7 + -5 – (7 – 5) = -2

Ä    La suma de números enteros tiene las propiedades siguientes:

Ø  Asociativa:

(a + b) + c = a + (b + c)

Ø  Conmutativa:

     a + b = b + a

Ø  Elemento neutro: el cero es el elemento neutro de la suma

     a + 0 = a

Ø  Elemento Opuesto: todo un numero entero a, tiene un numero opuesto -a

     a + (a) = 0

Resta de Números Enteros:

Una resta de números enteros se puede resolver como si se tratara de una suma, pero con una particularidad:

El símbolo de la resta le cambia el signo a la cifra que le sigue:

Por lo que:

Si el número que se resta es positivo lo convierte en negativo.

Si el número que se resta es negativo lo convierte en positivo.

Vamos a ver a continuación cuatro posibles casos:

Ejemplos

(+10) − (−5) = (+10) + (+5) = +15

(−7) − (+6) = (−7) + (−6) = −13

(−4) − (−8) = (−4) + (+8) = +4

(+2) − (+9) = (+2) + (−9) = −7

Multiplicación de Números Enteros:

Para Multiplicar números enteros se multiplican sus valores absolutos y el resultado se deja con signo positivo(+) si ambos factores son del mismo signo o se le coloca el signo menos(-) si los factores son de signos distintos.

Ä    La Multiplicación de números enteros tiene las propiedades siguientes:

Ø  Asociativa:

(a x b) x c = a x (b x c)

Ø  Conmutativa:

     a x b = b x a

Ø  Elemento neutro: el 1 es el elemento neutro de la multiplicación:

     a x 1 = a

Ø  Distributiva de la multiplicación respecto de la Suma:

     a x (b + c) = a x b + a x c

División de Números Enteros:

Para hallar el cociente exacto de dos números enteros se dividen sus valores

absolutos; si el dividendo y el divisor tienen igual signo, el cociente es positivo,

y si el dividendo y el divisor tienen distinto signo, el cociente es negativo.

Ejemplos:

10 : 5 = 2

(−10) : (−5) = 2

10 : (−5) = −2

(−10) : 5 = −2